11258. Number of rectangles
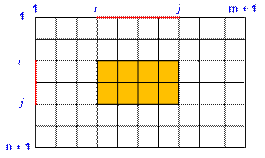
The grid consists of n * m unit
squares. How many different rectangles can be drawn on it?
The sides of the rectangles must be
parallel to the grid lines, and each rectangle should cover an integer number
of unit squares. Two rectangles of the same size are considered different if
they are located in different positions on the grid.
Input. Two positive integers n and m (n, m ≤
105).
Output. Print the number of different rectangles that can be
drawn on the grid.
|
Sample
input |
Sample
output |
|
2 3 |
18 |
SOLUTION
combinatorics
Algorithm analysis
Consider the
size of a rectangle a * b drawn on the grid. Let’s examine how many ways
we can choose the value of a. The grid contains n rows of
squares, and therefore there are n + 1 horizontal lines in the grid. Let’s number them
from 1 to n + 1.
We choose two
lines i and j (i < j). Drawing a segment between them forms the vertical
side a of the rectangle. The
number of ways to choose two numbers i and j (i < j) from the set {1, 2, …, n + 1} is
equal to ![]() . For example, for n =
2 there are 3 options to choose the vertical side of the rectangle:
. For example, for n =
2 there are 3 options to choose the vertical side of the rectangle:
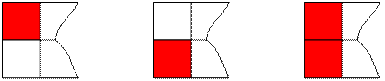
Similarly, the
grid has m + 1 vertical lines. The number of ways to select the
horizontal side of a rectangle is ![]() .
.
Therefore the
number of different rectangles on the grid is equal to
![]() *
* ![]() =
= ![]()
Example
For a 2 * 3
rectangle there are:
·
6 rectangles of size 1 * 1;

·
4 rectangles of size 1 * 2;

·
2 horizontal rectangles 1 * 3;
·
3 vertical rectangles 2 * 1;

·
2 rectangles 2 * 2;
·
1 rectangle 2 * 3;

The total result is ![]() *
* ![]() = 3 * 6 = 18 rectangles.
= 3 * 6 = 18 rectangles.
Algorithm implementation
Since
n, m ≤ 105, the
number of rectangles can be as large as ![]() *
* ![]() ≤ (105)2 * (105)2
= 1020. This result is beyond the bounds of a 64-bit integer. Therefore,
let’s implement the solution in Python.
≤ (105)2 * (105)2
= 1020. This result is beyond the bounds of a 64-bit integer. Therefore,
let’s implement the solution in Python.
n, m = map(int,input().split())
a = (n + 1) * n
// 2
b = (m + 1) * m
// 2
res = a * b
print(res)